- Free Matchmaking Horoscope Marriage
- Free Matchmaking Sites India
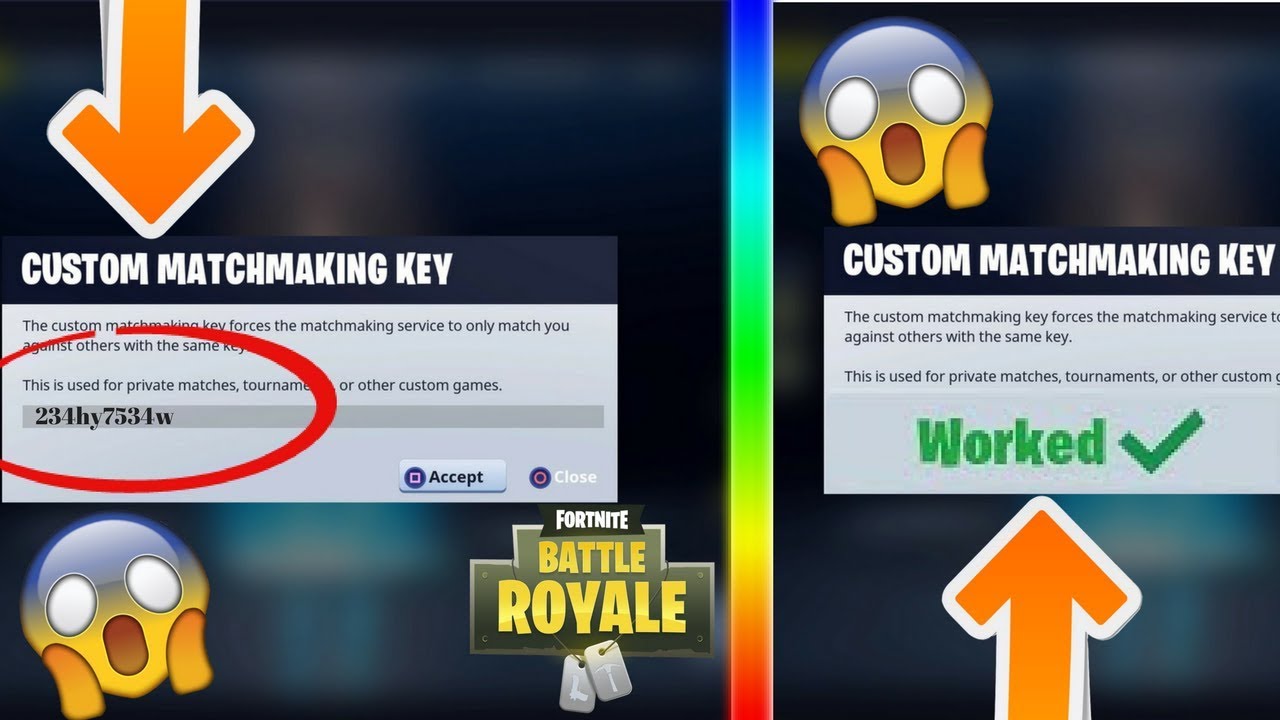
- Free Matchmaking Key Fortnite
- Free Matchmaking Astrology
- Free Matchmaking Services
Enter the birth details of the Boy and Girl in the form below. Marriage horoscope matching will be done online and porutham or marriage compatibility will be displayed as the result. Marriage matching is done based on the birth stars and janma rashi of the people getting married.
Check Porutham - Free Online Marriage Porutham Finder

Marriage matching or match making is a solemn decision taken on behalf of the boy and a girl before they tie the knot to hold and to behold each other for the rest of their lives. The Hindus ensure that the compatibility of this solemn lifelong binding enables the couple to live 'happily ever after'.

Count and match the numbers free and matching fun activities for children in preschool, kindergarten and first grade. These Matching objects worksheets will help children (Preschool/Nursery) to practice their thinking skills and fine motor skills. With Beginner level worksheets, students are asked to match terms to the given pictures.
Free Matchmaking Horoscope Marriage
- PopFlash is the easiest way to run a 5v5 CS:GO match on high quality 128 tick servers. No configuration, just click and go!
- Find your perfect match After adding your personal profile, browse through profiles of other Christian singles who are looking to make a new connection. Finding someone with similar interests and values has never been easier. ChristianDate.com is committed to building the most comprehensive free Christian dating service on the Internet.
Free Matchmaking Sites India

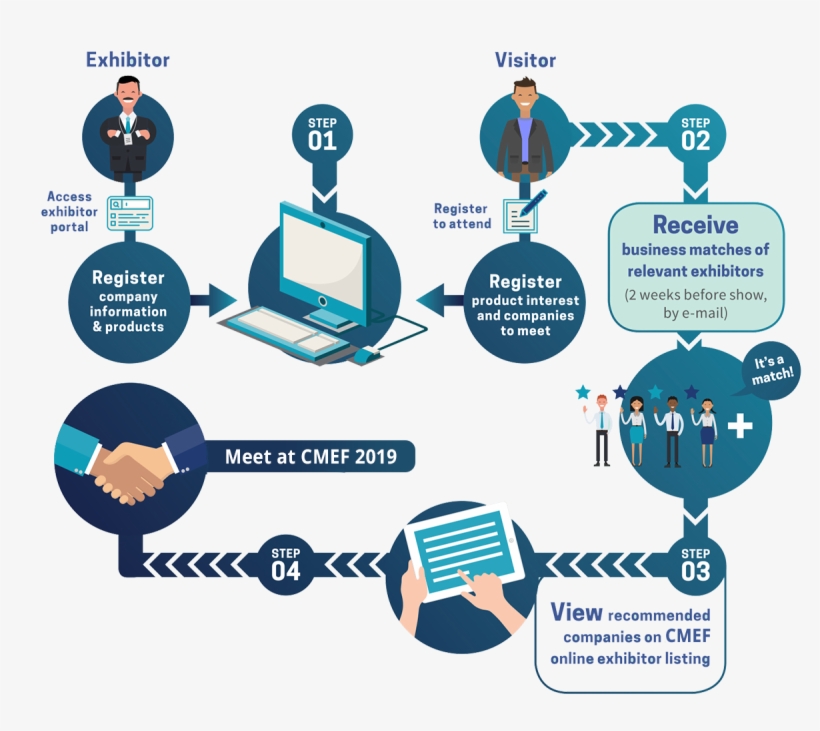
For this vital decision of their lives, the parents of both the girl and the boy who are to get married and the elders of their families get together; they then follow an ancient method, laid down by the sages of old, to see the marriage compatibility between the girl and the boy. This method is called ‘Porutham' or koota agreement.
Poruthams are chalked out after the study of the birth stars of both the boy and the girl who are contemplating marriage. The sages had initially devised 20 poruthams but now only 10 are in use. According to them, there are 27 birth stars (nakshatras) for each person in an oval configuration which constitutes a zodiac. The zodiac influences the person through the nine planets (navgrahas).
The 10 poruthams (kootas) thus chalked out are: dinam, ganam, yoni, rasi, rasiyathipaty, rajju, vedha, vasya, mahendram and stree deergham.
In economics and social choice theory, an envy-free matching (EFM) is a matching between people to 'things', which is envy-free in the sense that no person would like to switch his 'thing' with that of another person. This term has been used in several different contexts.
In unweighted bipartite graphs[edit]
In an unweighted bipartite graph G = (X+Y, E), an envy-free matching is a matching in which no unmatched vertex in X is adjacent to a matched vertex in Y.[1] Suppose the vertices of X represent people, the vertices of Y represent houses, and an edge between a person x and a house y represents the fact that x is willing to live in y. Then, an EFM is a partial allocation of houses to people such that each house-less person does not envy any person with a house, since he/she does not like any allocated house anyway.
Every matching that saturates X is envy-free, and every empty matching is envy-free. Moreover, if |NG(X)| ≥ |X| ≥ 1 (where NG(X) is the set of neighbors of X in Y), then G admits a nonempty EFM.[1] This is a relaxation of Hall's marriage condition, which says that, if |NG(X')| ≥ |X'| for every subset X' of X, then an X-saturating matching exists.
In markets with money[edit]
Consider a market in which there are several buyers and several goods, and each good may have a price. Given a price-vector, each buyer has a demand set - a set of bundles that maximize the buyer's utility over all bundles (this set might include the empty bundle, in case the buyer considers all bundles as too expensive).
A price-envy-free matching (given a price-vector) is a matching in which each agent receives a bundle from his demand-set. This means that no agent would prefer to get another bundle with the same prices.[2] An example of this setting is the rental harmony problem - matching tenants (the agents) to rooms (the items) while setting a price to each room.
Hull dating sites area. An envy-free price is a price-vector for which an envy-free matching exists. It is a relaxation of a Walrasian equilibrium: a Walrasian equilibrium consists of an EF price and EF matching, and in addition, every item must either be matched or have zero price. It is known that, in a Walrasian equilibrium, the matching maximizes the sum of values, i.e., it is a maximum-weight matching. However, the seller's revenue might be low. This motivates the relaxation to EF pricing, in which the seller may use reserve prices to increase the revenue; see envy-free pricing for more details.
In markets without money[edit]
The term envy-free matching is often used to denote a weaker condition - no-justified-envy matching.
Marriage matching or match making is a solemn decision taken on behalf of the boy and a girl before they tie the knot to hold and to behold each other for the rest of their lives. The Hindus ensure that the compatibility of this solemn lifelong binding enables the couple to live 'happily ever after'.
Count and match the numbers free and matching fun activities for children in preschool, kindergarten and first grade. These Matching objects worksheets will help children (Preschool/Nursery) to practice their thinking skills and fine motor skills. With Beginner level worksheets, students are asked to match terms to the given pictures.
Free Matchmaking Horoscope Marriage
- PopFlash is the easiest way to run a 5v5 CS:GO match on high quality 128 tick servers. No configuration, just click and go!
- Find your perfect match After adding your personal profile, browse through profiles of other Christian singles who are looking to make a new connection. Finding someone with similar interests and values has never been easier. ChristianDate.com is committed to building the most comprehensive free Christian dating service on the Internet.
Free Matchmaking Sites India
For this vital decision of their lives, the parents of both the girl and the boy who are to get married and the elders of their families get together; they then follow an ancient method, laid down by the sages of old, to see the marriage compatibility between the girl and the boy. This method is called ‘Porutham' or koota agreement.
Poruthams are chalked out after the study of the birth stars of both the boy and the girl who are contemplating marriage. The sages had initially devised 20 poruthams but now only 10 are in use. According to them, there are 27 birth stars (nakshatras) for each person in an oval configuration which constitutes a zodiac. The zodiac influences the person through the nine planets (navgrahas).
The 10 poruthams (kootas) thus chalked out are: dinam, ganam, yoni, rasi, rasiyathipaty, rajju, vedha, vasya, mahendram and stree deergham.
In economics and social choice theory, an envy-free matching (EFM) is a matching between people to 'things', which is envy-free in the sense that no person would like to switch his 'thing' with that of another person. This term has been used in several different contexts.
In unweighted bipartite graphs[edit]
In an unweighted bipartite graph G = (X+Y, E), an envy-free matching is a matching in which no unmatched vertex in X is adjacent to a matched vertex in Y.[1] Suppose the vertices of X represent people, the vertices of Y represent houses, and an edge between a person x and a house y represents the fact that x is willing to live in y. Then, an EFM is a partial allocation of houses to people such that each house-less person does not envy any person with a house, since he/she does not like any allocated house anyway.
Every matching that saturates X is envy-free, and every empty matching is envy-free. Moreover, if |NG(X)| ≥ |X| ≥ 1 (where NG(X) is the set of neighbors of X in Y), then G admits a nonempty EFM.[1] This is a relaxation of Hall's marriage condition, which says that, if |NG(X')| ≥ |X'| for every subset X' of X, then an X-saturating matching exists.
In markets with money[edit]
Consider a market in which there are several buyers and several goods, and each good may have a price. Given a price-vector, each buyer has a demand set - a set of bundles that maximize the buyer's utility over all bundles (this set might include the empty bundle, in case the buyer considers all bundles as too expensive).
A price-envy-free matching (given a price-vector) is a matching in which each agent receives a bundle from his demand-set. This means that no agent would prefer to get another bundle with the same prices.[2] An example of this setting is the rental harmony problem - matching tenants (the agents) to rooms (the items) while setting a price to each room.
Hull dating sites area. An envy-free price is a price-vector for which an envy-free matching exists. It is a relaxation of a Walrasian equilibrium: a Walrasian equilibrium consists of an EF price and EF matching, and in addition, every item must either be matched or have zero price. It is known that, in a Walrasian equilibrium, the matching maximizes the sum of values, i.e., it is a maximum-weight matching. However, the seller's revenue might be low. This motivates the relaxation to EF pricing, in which the seller may use reserve prices to increase the revenue; see envy-free pricing for more details.
In markets without money[edit]
The term envy-free matching is often used to denote a weaker condition - no-justified-envy matching.
In cake-cutting[edit]
Free Matchmaking Key Fortnite
The term envy-free matching has also been used in a different context: an algorithm for improving the efficiency of envy-free cake-cutting.[3] King city dating events man.
See also[edit]
References[edit]
Free Matchmaking Astrology
- ^ abSegal-Halevi, Erel; Aigner-Horev, Elad (28 January 2019). 'Envy-free Matchings in Bipartite Graphs and their Applications to Fair Division'. arXiv:1901.09527 [cs.DS].
- ^Alaei, Saeed; Jain, Kamal; Malekian, Azarakhsh (24 June 2010). 'Competitive Equilibria in Two Sided Matching Markets with Non-transferable Utilities'. arXiv:1006.4696 [cs.GT].
- ^Sen, Sandip; Nuchia, Stephen W. (1 August 2001). Improving Optimality of n Agent Envy-Free Divisions. Intelligent Agents VIII. Lecture Notes in Computer Science. 2333. Springer, Berlin, Heidelberg. pp. 277–289. doi:10.1007/3-540-45448-9_20. ISBN978-3-540-43858-8.
